Vol. 17 N° 2
Julio - Diciembre 2025
Este artículo presenta un estudio empírico de un teorema acerca de los números primos que es poco estudiado: “Todo número primo mayor que 3 equivale a un múltiplo de 6 aumentado o disminuido en una unidad”. Este teorema demostrado hace mucho tiempo indica que los números primos se pueden escribir como 6K — 1 o 6K + 1, con K un número entero positivo; pero, existen muchos valores de K para ambas formas que no generan números primos. Esta investigación se centra en las características o patrones de estos valores K que no generan números primos para las dos formas. La investigación demuestra que estos valores de K son infinitas progresiones aritméticas cuyas razones son números primos menores. Este descubrimiento permite generalizar los números primos a través de una criba con las restricciones de los valores de K; y a su vez, se logra demostrar la Conjetura de Goldbach (“todo número par mayor que 2, puede ser escrito como la suma de dos números primos”) con simplicidad de cálculos y a deducir tres corolarios de la misma.
This paper presents an empirical study of a theorem about prime numbers that is little studied: "Every prime number greater than 3 equals a multiple of 6 increased or decreased by one unit." This long-proven theorem indicates that prime numbers can be written as 6K — 1 or 6K + 1 , with k a positive integer, but there are many K-values for both forms that do not generate prime numbers. This research focuses on the characteristics or patterns of these K-values that do not generate prime numbers for the two forms. The research shows that these values of K are infinite arithmetic progressions whose ratios are smaller prime numbers. This discovery allows the generalization of prime numbers through a sieve with the constraints of the values of K; and in turn, it is possible to prove the Goldbach Conjecture ("every even number greater than 2 can be written as the sum of two prime numbers") with simplicity of calculations and to deduce three corollaries from the same values of K are infinite arithmetic progressions whose ratios are smaller prime numbers. This discovery allows the generalization of prime numbers through a sieve with the constraints of the values of K; and in turn, it is possible to prove the Goldbach Conjecture ("every even number greater than 2 can be written as the sum of two prime numbers") with simplicity of calculations and to deduce three corollaries from the same.
Los números primos han sido objeto de estudio y fascinación en la teoría de números debido a su relevancia como los "bloques fundamentales" en la construcción del conjunto de los números naturales. Entre estos resultados fundamentales, se encuentra el teorema que afirma que todo número primo mayor que 3 puede expresarse como un múltiplo de 6 aumentado o disminuido en la unidad. Este teorema, aunque simple en apariencia, abre una ventana hacia el análisis de patrones estructurales de los números primos y su relación con aquellos que poseen esta misma forma pero que no son primos.
El presente estudio se enfoca en identificar y analizar los patrones en los números de la forma 6K + 1 y 6K — 1 que no son primos, con el objetivo de explorar si estas regularidades pueden contribuir a una generalización que caracterice a los números primos en términos más amplios. Adicionalmente, se examina cómo dichos patrones pueden ofrecer nuevas perspectivas para abordar la histórica Conjetura de Goldbach, la cual plantea que todo número par mayor que 2 puede expresarse como la suma de dos números primos. El enfoque metodológico empleado es de naturaleza inductiva, partiendo de la observación de casos particulares para construir una generalización considerable.
Definición: Se dice que un número entero p > 1 es primo si sus únicos divisores son 1 y p, es decir, no existe divisor d de p tal que 1 < d < p. Si un número a > 1 no es primo se dice que es un número compuesto.
Los primeros números primos son: 2,3,5,7,13,17,19,23,29,31,37,41,43,47,53,...
Teorema 1: Todo número primo mayor que 3 equivale a un múltiplo de 6 aumentado o disminuido en una unidad. Es decir que todo número primo p > 3, p = 6K — 1 o p = 6K + 1 con K un número entero positivo.
Demostración
Sea p un número primo mayor que 3, demostraremos que p = 6K — 1 o p = 6K + 1 con K un número entero positivo.
En efecto dividamos p entre 6, sea K el cociente y r el residuo tendremos p = 6K + r siendo 6 el divisor. Ver los casos:
Ver algunos ejemplos
5 = 6.1 — 1
7 = 6.1 + 1
11 = 6.2 — 1
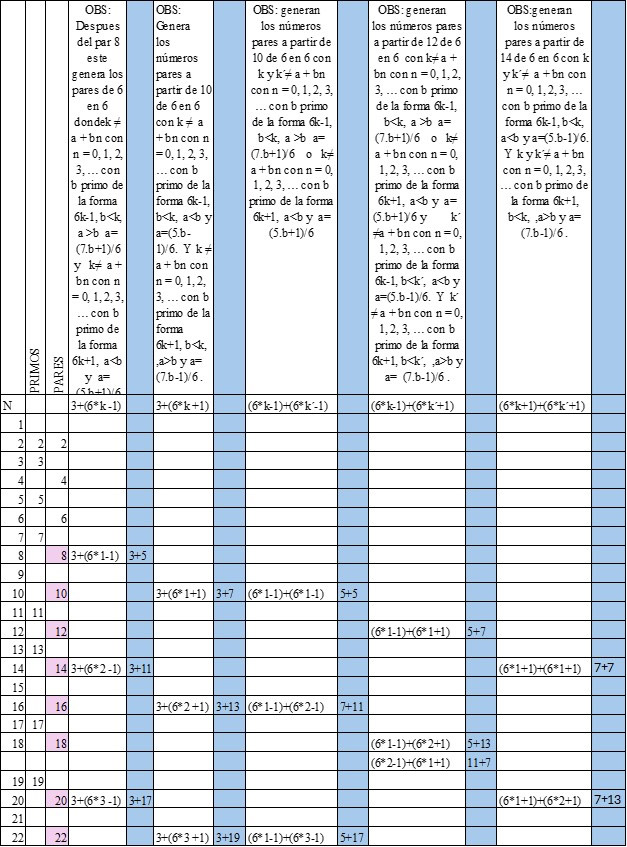
2.1. No todos los valores de K enteros positivos generan números primos para 6K — 1 y 6K + 1.
Tabla I. Números de la forma 6K — 1 y 6K + 1 ordenados en gráfico que llamaré gráfico de espiga colocada en horizontal, en el tallo se colocan los valores de K , arriba de K el valor de 6K — 1 y debajo de K el valor de 6K + 1. Resaltado en verde están los números primos
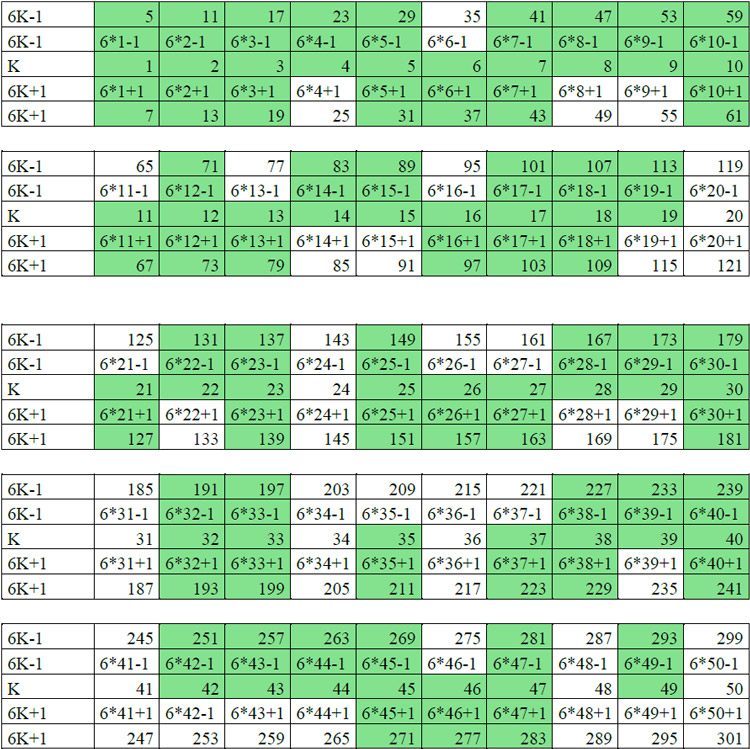
Revisar los valores de K que no generan números primos para la forma 6K — 1. Estos son:

¿Qué tienen en común estos números?

Observación 1: Los números que están en rojo: 6, 11, 16, 21, 26, 31, 36, 41, 46, 51, 56, 61, 66, 71, 76, 81, 86, 91, 96, 101, 106,… tienen en común que todos terminan en 1 y en 6, pero eso no es lo relevante, lo importante es que todos se pueden escribir como K = 6 + 5n, que es una progresión aritmética PA de razón 5. Para n = 0,1,2,3,4,... y podemos demostrar que generan a todos los múltiplos de 5 que tienen la forma 6K — 1 ¿Qué sucede si se sustituye este valor de K = 6 + 5n en la forma 6K — 1?
Véase la demostración:

Como se puede observar el resultado es un múltiplo de 5, es decir queda demostrado que el conjunto de valores de K = 6 + 5n, para n = 0,1,2,3,4, genera a todos los múltiplos de 5 de la forma 6K — 1.
Observación 2: Los números que están en sombreado amarillo: 6, 13, 20, 27, 34, 41, 48, 55, 62, 69, 76, 83, 90, 97, 104, 111, 118, 125, 132, 139, 146, 153, 160, 167, 174, 181, 188, 195, 202, 209, 216, 223, 230, … forman una PA de valores de K que se puede escribir de la forma K = 6 + 7n para n = 0,1,2,3,4, con razón 7 y afirmo que estos valores generan todos los múltiplos de 7 que tienen la forma 6K — 1 . Ver la demostración:
6(6 + 7n) — 1 =
6.6 + 6.7n — 1 =
36 + 6.7n — 1 =
35 + 6.7n =
7.5 + 6.7n =
7(5 + 6n) ⸫
queda demostrado que los valores de K = 6 + 7n para n = 0,1,2,3,4, generan los múltiplos de 7 para los números de la forma 6K — 1.
3.1. Más progresiones aritméticas que generan números compuestos de la forma 6K — 1
De la misma manera, como se estudió en la parte anterior. Se puede agregar más Progresiones aritméticas de números K = a + bn, para n = 0,1,2,3,4, forman números compuestos de la forma 6K — 1 con las siguientes características:
Tabla II. Valores de K que generan números compuestos para la forma 6K - 1

En esta tabla se puede observar algunos patrones:

Desde luego, se puede observar que los valores de K = a + bn que generan números compuestos de la forma 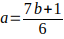 , ver:
, ver:
Cuando b = 5
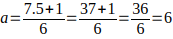 luego K = 6 + 5n con n = 0,1,2,3,..., este K genera todos los múltiplos de 5 de la forma
luego K = 6 + 5n con n = 0,1,2,3,..., este K genera todos los múltiplos de 5 de la forma
Cuando b = 11
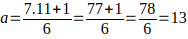 luego K = 13 + 11n con n = 0,1,2,3,...; este K genera todos los múltiplos de 11 de la forma 6k — 1, y así sucesivamente…
luego K = 13 + 11n con n = 0,1,2,3,...; este K genera todos los múltiplos de 11 de la forma 6k — 1, y así sucesivamente…
6(a + bn) — 1 = b(5 + 6n) despejar a de esta igualdad y queda:
Desde luego, se puede observar que los valores de K = a + bn que generan números compuestos de la forma 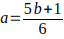 , véase:
, véase:
Cuando b = 7
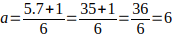 luego K = 6 + 7n con n = 0,1,2,3..., este K genera todos los múltiplos de 7 de la forma
luego K = 6 + 7n con n = 0,1,2,3..., este K genera todos los múltiplos de 7 de la forma
Cuando b = 13
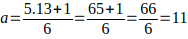 luego K = 11 + 13n con n = 0,1,2,3; este K genera todos los múltiplos de 13 de la forma 6k — 1, y así sucesivamente…
luego K = 11 + 13n con n = 0,1,2,3; este K genera todos los múltiplos de 13 de la forma 6k — 1, y así sucesivamente…
Observar los valores de K que no generan números primos para la forma
 , estos son:
, estos son:
4, 8, 9, 14, 15, 19, 20, 22, 24, 28, 29, 31, 34, 36, 39, 41, 42, 43, 44, 48, 49, 50, 53, 54, 57, 59, 60, 64, 65, 67, 69, 71, 74, 75, 78, 79, 80, 82, 84, 85, 86, 88, 89, 92, 93, 94, 97, 98, 99, 104, 106, 108, 109, 111, 113, 114, 116, 117, 119, 120, 124, 127, 129, 130, 132, 133, 134, 136, 139, …
Realizando observaciones similares a las anteriores se encuentra que:
Observación 1: Los números 4, 9, 14, 19, 24, 29, 34, 39, 44, 49, … es una progresión aritmética de valores de K que se pueden escribir de la forma
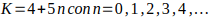 y forman los múltiplos de 5 para los números de la forma
y forman los múltiplos de 5 para los números de la forma  .
.
Ver la demostración
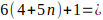 …
…
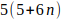 ⸫ Los valores de
⸫ Los valores de 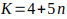 con
con 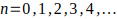 generan todos números de la forma
generan todos números de la forma  que son múltiplos de 5.
que son múltiplos de 5.
Observación 2: Los números 8, 15, 22, 29, 36, 43, 50, 57, 64, 71, … es una PA de los valores de K que se puede escribir de la forma
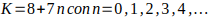 y razón 7 y forman los múltiplos de 7 para los números de la forma
y razón 7 y forman los múltiplos de 7 para los números de la forma  .
.
Demostración:
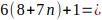 …
…
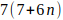 ⸫ Los valores de
⸫ Los valores de 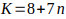 con
con  generan todos números de la forma
generan todos números de la forma  que son múltiplos de 7.
que son múltiplos de 7.
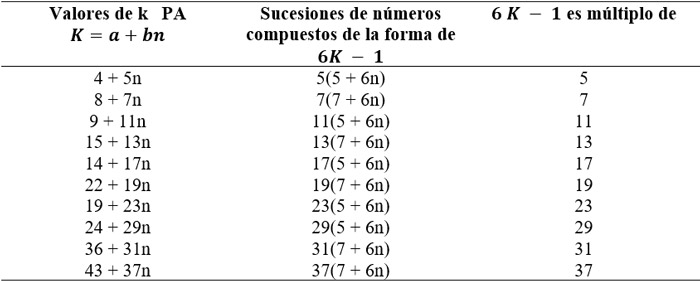
4.1 Más sucesiones de números K que generan números compuestos de la forma

Análogamente, se encuentra más Progresiones Aritméticas de valores de K que generan números compuestos de la forma
 . Ver
. Ver
Tabla III. Valores de K que generan números compuestos para la forma 6K + 1
4.2 Patrones observados en la tabla III:
 donde
b es un número primo y
donde
b es un número primo y
 y
y
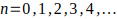 ,
y cada sucesión está formada por los números compuestos de la
forma 6K + 1 que son múltiplos de b.
,
y cada sucesión está formada por los números compuestos de la
forma 6K + 1 que son múltiplos de b.
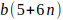 y
las otras de la forma
y
las otras de la forma
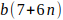 .
.
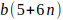 son los primos de la forma
son los primos de la forma
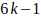 ,
es decir, 5, 11, 17, 23,… y los primos b que generan sucesiones de
números compuestos de la forma
,
es decir, 5, 11, 17, 23,… y los primos b que generan sucesiones de
números compuestos de la forma
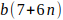 son los números primos que se pueden escribir como
son los números primos que se pueden escribir como
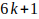 ,
es decir, 7, 13,19,31,37
,
es decir, 7, 13,19,31,37
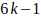 entonces
entonces
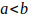 ;
si b es un primo de la forma
;
si b es un primo de la forma
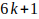 ,
entonces
,
entonces
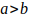 .
.
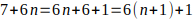 .
Sea
.
Sea
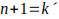 ,
entonces
,
entonces
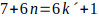 ,
es decir,
,
es decir,
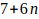 es un número de la forma
es un número de la forma
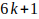 .
.
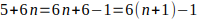 .
Sea
.
Sea
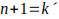 ,
entonces
,
entonces
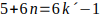 ,
es decir,
,
es decir,
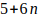 es
un número de la forma
es
un número de la forma
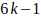 .
.
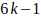 ,
el factor con que genera los múltiplos de b de la forma
,
el factor con que genera los múltiplos de b de la forma
 ,
son de la forma
,
son de la forma
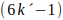 .
.
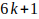 ,
el factor con que genera los múltiplos de b de la forma
,
el factor con que genera los múltiplos de b de la forma
 ,
son de la forma
,
son de la forma
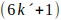 .
.
 ,
se obtiene multiplicando un número primo de la forma
,
se obtiene multiplicando un número primo de la forma
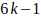 por otro (no necesariamente primo) de la misma forma y un número
primo de la forma
por otro (no necesariamente primo) de la misma forma y un número
primo de la forma
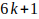 por
otro (no necesariamente primo) de la misma forma.
por
otro (no necesariamente primo) de la misma forma.
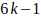 los múltiplos de b son
los múltiplos de b son
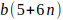 ,
luego para obtener el valor general de a sustituimos
,
luego para obtener el valor general de a sustituimos
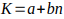 en
en
 y
queda:
y
queda:
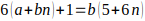 despejamos a de esta igualdad y queda
despejamos a de esta igualdad y queda
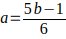
Desde luego, podemos observar que los valores de
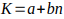 que generan números compuestos de la forma
que generan números compuestos de la forma  cuando b es de la forma
cuando b es de la forma 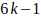 , es decir, 5,11, 17,.. tienen un valor de
, es decir, 5,11, 17,.. tienen un valor de 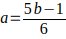 , veámoslo:
, veámoslo:
Cuando
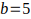
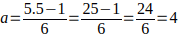 luego
luego 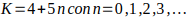 , este K genera todos los múltiplos de 5 de la forma
, este K genera todos los múltiplos de 5 de la forma 
Cuando
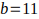
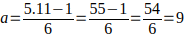 luego
luego 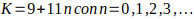 ; este K genera todos los múltiplos de 11 de la forma
; este K genera todos los múltiplos de 11 de la forma  , y así sucesivamente…
, y así sucesivamente…
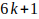 los múltiplos de b son
los múltiplos de b son
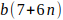 ,
luego para obtener el valor general de a sustituimos
,
luego para obtener el valor general de a sustituimos
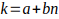 en
en
 y queda:
y queda:
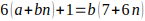 despejamos a de esta igualdad y queda
despejamos a de esta igualdad y queda
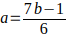
Desde luego, se puede observar que los valores de
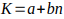 que generan números compuestos de la forma
que generan números compuestos de la forma  cuando b es de la forma
cuando b es de la forma 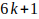 , es decir, 7,13, 19,.. tienen un valor de
, es decir, 7,13, 19,.. tienen un valor de 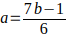 , véase:
, véase:
Cuando b=7
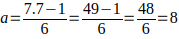 luego
luego 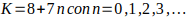 este K genera todos los múltiplos de 7 de la forma
este K genera todos los múltiplos de 7 de la forma 
Cuando b=13
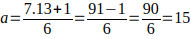 luego
luego 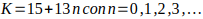 ; este K genera todos los múltiplos de 13 de la forma
; este K genera todos los múltiplos de 13 de la forma  , y así sucesivamente…
, y así sucesivamente…
Con el estudio realizado en la parte 3 y parte 4 se puede concluir que los números primos se pueden obtener con la siguiente fórmula o criba:

Nota: Para conocer los números primos mayores que 3 y menores o igual a un número N dado, basta con estudiar los valores de 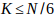 . Luego
. Luego 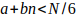 despejando n queda de cada caso será:
despejando n queda de cada caso será:
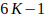 ,
se tiene dos opciones si b es de la forma
,
se tiene dos opciones si b es de la forma
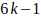 es
decir, 5,11,17,23.. o si b es de la forma
es
decir, 5,11,17,23.. o si b es de la forma
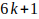 es decir, 7,13,19,31,. En el primer caso
es decir, 7,13,19,31,. En el primer caso
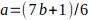
Entonces
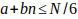
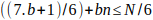
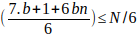
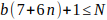
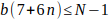
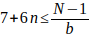
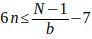
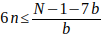
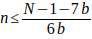
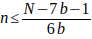 y despejando b quedarà
y despejando b quedarà
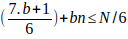
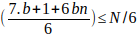
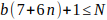
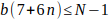
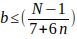 el mayor valor de b es cuando
el mayor valor de b es cuando 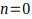 por lo tanto
por lo tanto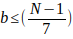
En el segundo caso si b es de la forma
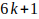 es decir, 7,13,19,31,. El valor de
es decir, 7,13,19,31,. El valor de 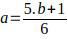 luego
luego
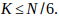
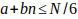
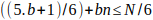
Despejando b queda
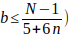 el mayor valor de b es cuando
el mayor valor de b es cuando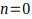 por lo tanto
por lo tanto 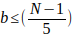
Despejando n queda
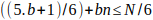
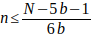
Nota: Usando los valores del primer caso se obtienen los mismos números compuestos del segundo caso.
 ,
se tendrán dos opciones si b es de la forma
,
se tendrán dos opciones si b es de la forma
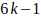 es
decir, 5,11,17,23.. o si b es de la forma
es
decir, 5,11,17,23.. o si b es de la forma
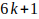 es decir, 7,13,19,31,. Realizando un estudio similar al anterior
se concluyen los siguientes despejes:
es decir, 7,13,19,31,. Realizando un estudio similar al anterior
se concluyen los siguientes despejes:
Ver el primer caso si b es de la forma
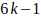 luego
luego 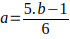
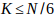 .
.
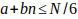
((5.b-1)/6) + bn ≤N/6
Despejando b queda
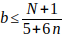 el mayor valor de b es cuando
el mayor valor de b es cuando 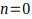 por lo tanto
por lo tanto 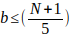
Despejando n queda
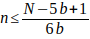
Segundo caso si
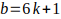 es decir, 7,13,19,31,
es decir, 7,13,19,31,
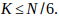
Despejando b queda
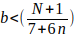 el mayor valor de b es cuando
el mayor valor de b es cuando 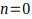 por lo tanto
por lo tanto 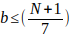
despejando n queda
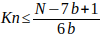
La presente investigación sobre los números primos se desarrolla a partir de un enfoque inductivo, utilizando la observación de casos particulares para establecer generalizaciones y detectar patrones estructurales en números de la forma 6K + 1 y 6K — 1.
Todo número primo mayor que 3 equivale a un múltiplo de 6 aumentado o disminuido en una unidad. Es decir que todo número primo p >3 , p = 6K-1 o p= 6K+1 con K un número entero positivo, siempre que:
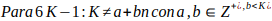 ,
,
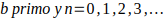 ; si b es un primo de la forma 6k-1, a>b y
; si b es un primo de la forma 6k-1, a>b y
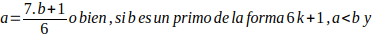
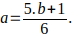
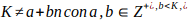
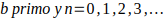 ; si b es un primo de la forma 6k – 1,
; si b es un primo de la forma 6k – 1,
 .
.
Demostración
Con el teorema 1 queda claro que los números primos mayores que 3 tienen dos formas de escribirse estas son
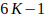 y
y  . Pero también, que hay números de esas dos formas que no son primos, estos serían los números que resulten del producto de un primo de la forma
. Pero también, que hay números de esas dos formas que no son primos, estos serían los números que resulten del producto de un primo de la forma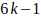 por otro (no necesariamente primo) de la forma
por otro (no necesariamente primo) de la forma 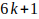 y viceversa, y uno de la forma
y viceversa, y uno de la forma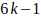 por otro igual (no necesariamente primo), y uno de la forma
por otro igual (no necesariamente primo), y uno de la forma 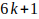 por otro igual (no necesariamente primo).
por otro igual (no necesariamente primo).
Ver el primer caso para la forma 6K — 1
Sea
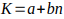 con
con 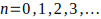 con b primo de la forma
con b primo de la forma 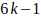 , es decir, 5,11,17, 23,…;
, es decir, 5,11,17, 23,…; 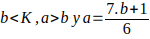 . Si sustituimos
. Si sustituimos
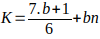 en la forma
en la forma
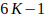 quedará
quedará
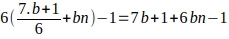
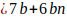
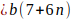
Recordar que b es primo de la forma
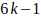 , luego para ese valor de K los múltiplos de b serán de la forma
, luego para ese valor de K los múltiplos de b serán de la forma 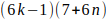 . Con n= 0,1,2,3,… Es decir, para ese valor de K, la forma
. Con n= 0,1,2,3,… Es decir, para ese valor de K, la forma 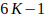 es un múltiplo de b. Por lo tanto, ese valor de K no genera números primos para la forma
es un múltiplo de b. Por lo tanto, ese valor de K no genera números primos para la forma 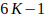 .
.
Ver el segundo caso para la forma 6K — 1
Sea
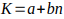 con n = 0, 1, 2, 3, … con b primo de la forma
con n = 0, 1, 2, 3, … con b primo de la forma 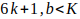 es decir, 7,13,19;
es decir, 7,13,19; 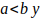
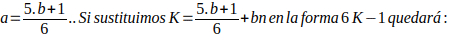
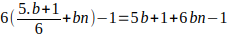
= 5b + 6bn
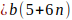
Recordar que b es primo de la forma
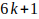 , luego para ese valor de K los múltiplos de b serán de la forma
, luego para ese valor de K los múltiplos de b serán de la forma 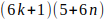 con n= 0,1,2,3,… Es decir, para ese valor de K, la forma
con n= 0,1,2,3,… Es decir, para ese valor de K, la forma 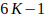 es un múltiplo de b. Por lo tanto, ese valor de K no genera números primos para la forma
es un múltiplo de b. Por lo tanto, ese valor de K no genera números primos para la forma 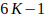 .
.
Véase el primer caso para la forma 6K + 1
Sea
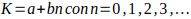 con b primo de la forma
con b primo de la forma 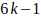 , es decir, 5,11,17, 23,…;
, es decir, 5,11,17, 23,…; 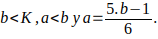
Al sustituir
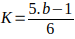 + bn en la forma 6K + 1 quedará:
+ bn en la forma 6K + 1 quedará:
6(
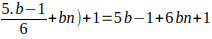
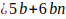
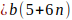
Como que b es primo de la forma
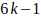 , luego para ese valor de K los múltiplos de b serán de la forma
, luego para ese valor de K los múltiplos de b serán de la forma 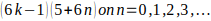 Es decir, para ese valor de K, la forma
Es decir, para ese valor de K, la forma  es un múltiplo de b. Por lo tanto, ese valor de K no genera números primos para la forma
es un múltiplo de b. Por lo tanto, ese valor de K no genera números primos para la forma  .
.
Véase el segundo caso para la forma 6K + 1
Sea
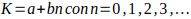 con b primo de la forma
con b primo de la forma 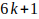 , es decir, 7,13,19;
, es decir, 7,13,19;
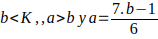
Si se sustituye
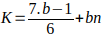 en la forma
en la forma
 quedará:
quedará:
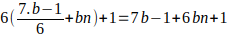
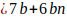
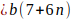
Siendo que b es primo de la forma
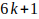 , luego para ese valor de K los múltiplos de b serán de la forma
, luego para ese valor de K los múltiplos de b serán de la forma 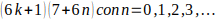 Es decir, para ese valor de K, la forma
Es decir, para ese valor de K, la forma  es un múltiplo de b. Por lo tanto, ese valor de K no genera números primos para la forma
es un múltiplo de b. Por lo tanto, ese valor de K no genera números primos para la forma  .
.
Con la demostración del teorema 1 (ya conocido) se ha visto que todos los números primos mayores que 3 se pueden escribir como
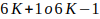 con K un número entero positivo. Y con el teorema 2 planteado, se ha encontrado las excepciones de K que no generan números primos para esas dos formas, y con estas demostraciones se tiene una criba que deja filtrar los números primos. Y queda demostrado que: los números primos se pueden obtener con la siguiente fórmula o criba:
con K un número entero positivo. Y con el teorema 2 planteado, se ha encontrado las excepciones de K que no generan números primos para esas dos formas, y con estas demostraciones se tiene una criba que deja filtrar los números primos. Y queda demostrado que: los números primos se pueden obtener con la siguiente fórmula o criba:

Para determinar los números primos mayores que 3 menores que un N cualquiera se procede de la siguiente manera: Se hallan los valores de 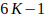 y
y  hasta
hasta 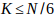 . Luego se descartan los siguientes valores:
. Luego se descartan los siguientes valores:
Para descartar los valores 6K-1 que no son primos
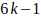 )
con la fórmula
)
con la fórmula
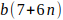 dando valores a b desde 5 hasta
dando valores a b desde 5 hasta
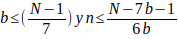 ;
;
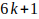 )
con la fórmula
)
con la fórmula
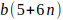 dando valores a b desde 7 hasta
dando valores a b desde 7 hasta
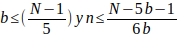
Para descartar los valores 6k+1 que no son primos
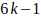 )
con la fórmula
)
con la fórmula
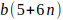 dando valores a b desde 5 hasta
dando valores a b desde 5 hasta
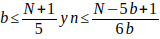 ; Como b es de la forma
; Como b es de la forma
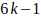 si
si
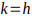 ,
n se comienza a estudiar desde
,
n se comienza a estudiar desde
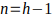 y
se deja de estudiar hasta el máximo valor de n para dicho b con la
fórmula
y
se deja de estudiar hasta el máximo valor de n para dicho b con la
fórmula
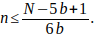 El
estudio termina cuando para un
El
estudio termina cuando para un
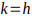 el máximo valor de n es igual al mínimo , es decir, el estudio
comienza con
el máximo valor de n es igual al mínimo , es decir, el estudio
comienza con
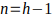 y termina con
y termina con
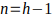 .
.
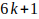 con la fórmula
con la fórmula
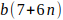 dando valores a b desde 7 hasta
dando valores a b desde 7 hasta
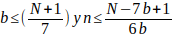 ;
Como b es de la forma
;
Como b es de la forma
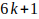 si
si
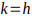 ,
n se comienza a estudiar desde n=h-1y se deja de estudiar hasta el
máximo valor de n para dicho b con la fórmula
,
n se comienza a estudiar desde n=h-1y se deja de estudiar hasta el
máximo valor de n para dicho b con la fórmula
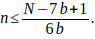 El
estudio termina cuando para un
El
estudio termina cuando para un
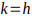 el máximo valor de n es igual al mínimo , es decir, el estudio
comienza con
el máximo valor de n es igual al mínimo , es decir, el estudio
comienza con
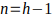 y termina con
y termina con
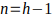 .
.
La Conjetura de Goldbach es una de las conjeturas más famosas en la teoría de números. Fue propuesta por el matemático prusiano Christian Goldbach en 1742 y afirma que:
Conjetura de Goldbach: Todo número par mayor que 2, puede ser escrito como la suma de dos números primos.
Demostración: Sean los números primos mayores que 3. Estos pueden representarse en una de las dos formas congruenciales:
p≡±1(mod6), es decir, p = 6K−1 o p = 6K+1 para alguˊn entero K
Según los Teoremas 1 y 2, se impone una condición adicional sobre los valores de K, definidos por expresiones del tipo:
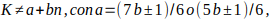 según corresponda a la forma del primo b.
según corresponda a la forma del primo b.
Los números primos no incluidos en el teorema 1 y 2 son los números 2 y 3.
Ver los casos
Sea un número par N mayor que 3, N se puede escribir como la suma de dos números primos, Ver los casos
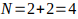 es
par
es
par
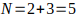 no
es par
no
es par
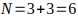 es par
es par
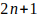 le sumamos 2 será
le sumamos 2 será
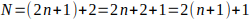 es impar.
es impar.
Ver los demás casos.,
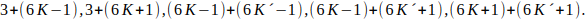
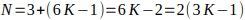 es
par
es
par
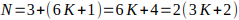 es par
es par
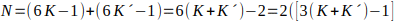 es par
es par
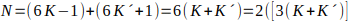 es par
es par
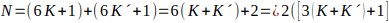 es
par.
es
par.
Todas estas sumas son pares, por lo que se cumple que la suma de dos primos de estas formas genera un número par.
Si asumimos la infinitud de primos en ambas clases congruenciales y los valores de K compatibles según las restricciones dadas por los Teoremas 1 y 2, entonces cualquier número par mayor que 6 puede expresarse como la suma de dos números primos bajo alguna de las combinaciones descritas arriba. Por lo tanto cualquier número par mayor que 2 , puede ser escrito como la suma de dos números primos. Estos son:
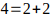
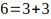
Los demás números pares mayores que 6 pueden ser escritos de una o más de las siguientes maneras

Y así queda demostrada la Conjetura de Goldbach.
Ver los primeros ejemplos en la siguiente tabla
Tabla IX. Números pares del 8 al 100, escritos como suma de dos números primos

Demostración



Demostración



Demostración

En el desarrollo de la presente investigación, se ha establecido un método de criba que permite extender la definición y caracterización de los números primos, proporcionando un marco teórico que permite abordar la demostración de la conjetura de Goldbach. Durante la implementación del procedimiento, se realizó una discriminación sobre los valores de k y k′', lo que asegura la validez de los resultados obtenidos. No obstante, los valores de n no fueron discriminados, lo que permite la aparición de valores repetidos dentro del conjunto analizado. A pesar de ello, esta repetición no impacta la integridad de los hallazgos, ya que la estructura de la criba y las relaciones matemáticas establecidas preservan la coherencia lógica de los resultados.
Adicionalmente, la formulación del presente estudio ha dado lugar a la aparición de un conjunto de ecuaciones diofánticas específicas. Se plantea que el análisis detallado de estas ecuaciones, junto con la exploración de métodos eficientes para su resolución, podría derivar en el desarrollo de un algoritmo práctico capaz de determinar la primalidad de cualquier número entero positivo de manera sistemática.
La presente investigación ha desarrollado un método de criba que generaliza los números primos y aporta un marco teórico que logra la demostración de la conjetura de Goldbach. Además, la aparición de ecuaciones diofánticas específicas sugiere la posibilidad de diseñar un algoritmo eficiente para determinar la primalidad de los números enteros, En futuras investigaciones, sería conveniente estudiar estrategias óptimas para la resolución de estas ecuaciones diofánticas, considerando tanto métodos algebraicos como numéricos, con el fin de determinar patrones que faciliten la verificación de la primalidad de los números enteros.
Apostol, T. ( 1984) Introducción a la teoría analítica de los números. Editorial Reverté. Caracas. Venezuela.
Baldor, A. (1944). Aritmética teórico-practica. Habana , Cuba : Cultural,SA.
Castellano, Z (2022) Criba eficiente secuencia de raíz digital tesla Zollner números primos y compuestos. TECSZOLL. C.A. Valencia Venezuela. https://www.researchgate.net/publication/364039609_TEST_DE_PRIMALIDAD_DE_SECUENCIA_PRIMORDIAL_TESLA_ZOLLNER_NUMEROS_PRIMOS_Y_COMPUESTOS
Guevara Bravo, J. César y Ojeda Uresti, Juan. (2006). ¿Formuló Goldbach la conjetura de Goldbach? Ciencias 81, enero-marzo, 72-79. https://www.revistacienciasunam.com/es/54-revistas/revista-ciencias-81/349-iformulo-goldbach-la-conjetura-de-goldbach-.html
Granville A. y Martin G. (2005). Carrera de números primos. El diablo de los números. LA GACETA DE LA RSME, 8(1), 197–240. https://matematicas.uam.es/~franciscojavier.cilleruelo/Curso/Carreras.pdf (Posible: Revisar)
Mora, W. (2010) Introducción a la teoría de números. Ejemplos y algoritmos. Revista digital Matemática Educación e Internet. Segunda Edición. Costa Rica. www.tec-digital.itcr.ac.cr/revistamatematica/
Niven, I. y Zuckerman, H. (1976) Introducción a la teoría de los números. Editorial Limusa . México